手性向列膠體中可重構的打結和連接

（2011 Science文章）

對高聚物，大分子或者復雜材料中的缺陷線的打結或構建微尺度環是材料科學中富有挑戰性的任務。通過使用激光鑷作為一個顯微操控工具，將手性向列液晶膠體中的微觀拓撲缺陷線進行了任意復雜程度的打結和連接。所展示的所有結和連接包括霍普夫連接，大衛之星， 博羅梅安環都具有高達6個交叉， 并將膠體微粒穩定在不尋常的軟物質中。手性向列膠體中的結按照自連接的數量，幾何學的直接測量或Berry相進行分類。在手性向列膠體中構建任意微觀尺度結和連接展示了軟物質材料工程中拓撲學的重要性。

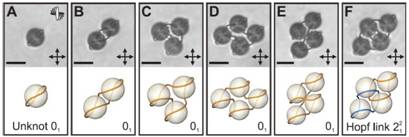
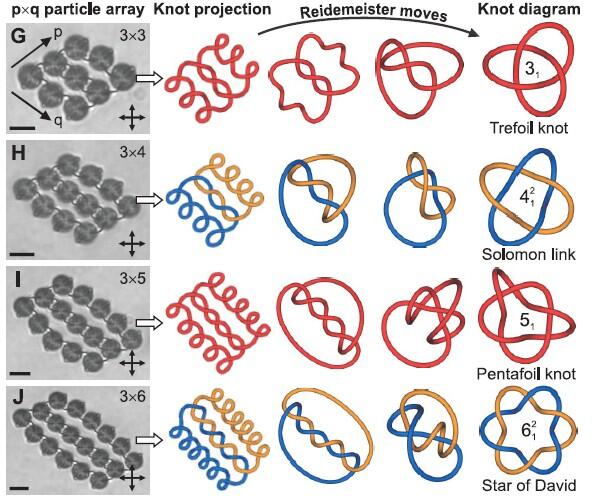
Fig. 1.手性向列膠體中拓撲缺陷線的打結和連接 (A) 一個扭曲的缺陷環拓撲學上等效于解結并自發的環繞著一個單獨的小球。該單元的頂部和底部的分子取向與正交偏光鏡的方向相同。 (B to E) 膠體二聚體，三聚體，四聚體缺陷環被等效解開。 (F) 使用兩個內連接缺陷環編織出第一個不尋常的霍普夫連接。在 (A) 到 (F)中, 相應環的構建通過朗道-德讓納模型量化計算. (13). (G to J) 在pxq微粒陣列上的一系列交替環形結和連接通過激光誘導的缺陷融合進行編織。使用一個打結程序再次描繪缺陷線（33）來展示從初始平面投影到最終打結圖解的圖像，這通過一系列的邁斯特移動來實現。結的命名使用標準方法Ci，N，其中C表明了交叉的最少數量，i用于區分不同結的類型，N表明多組分連接中環的數量。標尺，5um。

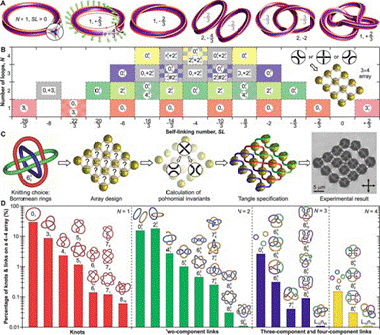
Fig. 3.連接和結的向列辮子的拓撲分類和定制組裝         (A) 缺陷環具有一個局部雙曲截面的3重旋轉對稱并對應于3帶面，類似于莫比斯環。 它們可以通過環數目N和自連接數目SL的分數值明確地標識出來。 (B) 3x4微粒陣列上的所有可能的結和連接通過SL和N進行分類。結和連接的分層次序，以不同的顏色和標準的符號顯示。 (C) Pxq微粒陣列上博羅梅安環的定制組裝.可行的扭結組合使用基于瓊斯多項式和考夫曼支架方法(24, 28)的數值算法測試.選擇的配置通過多項式直接比較，在Table of Knot Invariants（29）中枚舉出來并用激光鑷組裝。(D) 在4x4微粒陣列上的初級結和連接的分布展示了一個大的拓撲結構的多樣性，其最小交叉數高達10。發生一個特殊結或連接的可能性隨其復雜程度下降，復雜度由測得的最小交叉數決定。

原文請參考 

2011 science - Reconfigurable Knots and Links in Chiral NematicColloids